Millised näevad välja erinevate funktsioonide graafikud. Funktsioonid ja nende graafikud

Põhilised elementaarfunktsioonid, nendele omased omadused ja vastavad graafikud on matemaatikateadmiste üks põhialuseid, mis on oma tähtsuselt sarnane korrutustabeliga. Elementaarfunktsioonid on kõigi teoreetiliste küsimuste uurimise aluseks, toeks.

Allolev artikkel pakub põhimaterjali põhiliste elementaarfunktsioonide teemal. Tutvustame termineid, anname neile definitsioone; Uurime üksikasjalikult iga tüüpi elementaarfunktsioone ja analüüsime nende omadusi.

Eristatakse järgmist tüüpi põhilisi elementaarfunktsioone:

Definitsioon 1

konstantne funktsioon (konstant);
n-s juur;
toitefunktsioon;
eksponentsiaalne funktsioon;
logaritmiline funktsioon;
trigonomeetrilised funktsioonid;
vennalikud trigonomeetrilised funktsioonid.

Konstantne funktsioon defineeritakse valemiga: y = C (C on teatud reaalarv) ja sellel on ka nimi: konstant. See funktsioon määrab sõltumatu muutuja x mis tahes reaalväärtuse vastavuse muutuja y samale väärtusele - C väärtusele.

Konstandi graafik on sirgjoon, mis on paralleelne abstsissteljega ja läbib punkti, mille koordinaadid (0, C). Selguse huvides esitame konstantsete funktsioonide y = 5, y = - 2, y = 3, y = 3 graafikud (joonisel on märgitud vastavalt musta, punase ja sinise värviga).

2. definitsioon

See elementaarfunktsioon on defineeritud valemiga y = x n (n on ühest suurem naturaalarv).

Vaatleme funktsiooni kahte varianti.

n-s juur, n – paarisarv

Selguse huvides näitame joonist, mis näitab selliste funktsioonide graafikuid: y = x, y = x 4 ja y = x8. Need funktsioonid on värvikoodiga: vastavalt must, punane ja sinine.

Funktsioonigraafikud on sarnase välimusega ühtlane aste indikaatori muude väärtuste jaoks.

3. määratlus

N-nda juurfunktsiooni omadused, n on paarisarv

määratluspiirkond – kõigi mittenegatiivsete reaalarvude hulk [ 0 , + ∞) ;
kui x = 0, funktsioon y = x n väärtus on võrdne nulliga;
antud funktsioon-funktsioonüldvorm (ei ole paaris ega paaritu);
vahemik: [ 0 , + ∞) ;
see funktsioon y = x n paarisjuureastendajate korral suureneb kogu definitsioonipiirkonna ulatuses;
funktsioonil on kumerus ülespoole suunatud kogu definitsioonipiirkonna ulatuses;
pöördepunktid puuduvad;
asümptoote pole;
funktsiooni graafik paaris n korral läbib punkte (0; 0) ja (1; 1).

n-s juur, n – paaritu arv

Selline funktsioon on defineeritud kogu reaalarvude hulga kohta. Selguse huvides vaadake funktsioonide graafikuid y = x 3, y = x 5 ja x 9 . Joonisel on need tähistatud värvidega: must, punane ja sinine on vastavalt kõverate värvid.

Funktsiooni y = x n juureksponenti teised paaritud väärtused annavad sarnast tüüpi graafiku.

4. määratlus

N-nda juurfunktsiooni omadused, n on paaritu arv

määratluspiirkond – kõigi reaalarvude hulk;
see funktsioon on paaritu;
väärtuste vahemik – kõigi reaalarvude hulk;
funktsioon y = x n paaritute juureksponentide korral suureneb kogu definitsioonipiirkonna ulatuses;
funktsioonil on intervallil nõgusus (- ∞ ; 0 ] ja kumerus intervallil [ 0 , + ∞);
käändepunktil on koordinaadid (0; 0);
asümptoote pole;
Funktsiooni graafik paaritu n korral läbib punkte (- 1 ; - 1), (0 ; 0) ja (1 ; 1).

Toitefunktsioon

Definitsioon 5

Võimsusfunktsioon defineeritakse valemiga y = x a.

Graafikute välimus ja funktsiooni omadused sõltuvad eksponendi väärtusest.

kui astmefunktsioonil on täisarv astendaja a, siis astmefunktsiooni graafiku tüüp ja omadused sõltuvad sellest, kas astendaja on paaris või paaritu, samuti sellest, milline on astendaja märk. Vaatleme allpool kõiki neid erijuhtumeid üksikasjalikumalt;
eksponent võib olla murdosa või irratsionaalne – olenevalt sellest varieeruvad ka graafikute tüüp ja funktsiooni omadused. Erijuhtumeid analüüsime mitme tingimuse seadmisega: 0< a < 1 ; a > 1 ; - 1 < a < 0 и a < - 1 ;
võimsusfunktsioonil võib olla nullastendaja, analüüsime seda juhtumit ka allpool üksikasjalikumalt.

Analüüsime võimsusfunktsiooni y = x a, kui a on paaritu positiivne arv, näiteks a = 1, 3, 5...

Selguse huvides näitame selliste võimsusfunktsioonide graafikuid: y = x (graafiline värv must), y = x 3 (graafiku sinine värv), y = x 5 (graafiku punane värv), y = x 7 (graafiline värv roheline). Kui a = 1, saame lineaarfunktsiooni y = x.

Definitsioon 6

Positiivse astme funktsiooni omadused, kui astendaja on paaritu positiivne

funktsioon kasvab x ∈ korral (- ∞ ; + ∞) ;
funktsioonil on kumerus x ∈ (- ∞ ; 0 ] ja nõgusus x ∈ [ 0 ; + ∞) korral (v.a lineaarfunktsioon);
käändepunktil on koordinaadid (0 ; 0) (v.a lineaarfunktsioon);
asümptoote pole;
funktsiooni läbimise punktid: (- 1 ; - 1) , (0 ; 0) , (1 ; 1) .

Analüüsime võimsusfunktsiooni y = x a, kui a on paarisarv, näiteks a = 2, 4, 6...

Selguse huvides näitame selliste võimsusfunktsioonide graafikuid: y = x 2 (graafiline värv must), y = x 4 (graafiku sinine värv), y = x 8 (graafiku punane värv). Kui a = 2, saame ruutfunktsioon, mille graafik on ruutparabool.

Definitsioon 7

Positiivse astme funktsiooni omadused, kui astendaja on isegi positiivne:

määratluspiirkond: x ∈ (- ∞ ; + ∞) ;
väheneb x ∈ jaoks (- ∞ ; 0 ] ;
funktsioonil on nõgusus x ∈ jaoks (- ∞ ; + ∞) ;
pöördepunktid puuduvad;
asümptoote pole;
funktsiooni läbimise punktid: (- 1 ; 1) , (0 ; 0) , (1 ; 1) .

Alloleval joonisel on võimsusfunktsiooni graafikute näited y = x a, kui a on paaritu negatiivne arv: y = x - 9 (graafiline värv must); y = x - 5 (graafiku sinine värv); y = x - 3 (graafiku punane värv); y = x - 1 (graafiline värv roheline). Kui a = - 1, saame pöördvõrdelisuse, mille graafik on hüperbool.

Definitsioon 8

Astmefunktsiooni omadused, kui astendaja on paaritu negatiivne:

Kui x = 0, saame teist tüüpi katkestuse, kuna lim x → 0 - 0 x a = - ∞, lim x → 0 + 0 x a = + ∞ a = - 1, - 3, - 5, … korral. Seega on sirge x = 0 vertikaalne asümptoot;

vahemik: y ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
funktsioon on paaritu, sest y (- x) = - y (x);
funktsioon on kahanev x ∈ - ∞ korral; 0 ∪ (0 ; + ∞);
funktsioonil on kumerus x ∈ (- ∞ ; 0) ja nõgusus x ∈ (0 ; + ∞) korral;
pöördepunktid puuduvad;

k = lim x → ∞ x a x = 0, b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0, kui a = - 1, - 3, - 5, . . . .

funktsiooni läbimise punktid: (- 1 ; - 1) , (1 ; 1) .

Alloleval joonisel on näited astmefunktsiooni y = x a graafikutest, kui a on paarisarv: y = x - 8 (graafiline värv must); y = x - 4 (graafiku sinine värv); y = x - 2 (graafiku punane värv).

Definitsioon 9

Astmefunktsiooni omadused, kui eksponent on isegi negatiivne:

määratluspiirkond: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;

Kui x = 0, saame teist tüüpi katkestuse, kuna lim x → 0 - 0 x a = + ∞, lim x → 0 + 0 x a = + ∞ a = - 2, - 4, - 6, … korral. Seega on sirge x = 0 vertikaalne asümptoot;

funktsioon on paaris, sest y(-x) = y(x);
funktsioon kasvab x ∈ (- ∞ ; 0) ja väheneb x ∈ 0 korral; + ∞ ;
funktsioonil on nõgusus x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
pöördepunktid puuduvad;
horisontaalne asümptoot – sirge y = 0, sest:

k = lim x → ∞ x a x = 0, b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0, kui a = - 2 , - 4 , - 6 , . . . .

funktsiooni läbimise punktid: (- 1 ; 1) , (1 ; 1) .

Pöörake algusest peale tähelepanu järgmisele aspektile: juhul, kui a on paaritu nimetajaga positiivne murd, võtavad mõned autorid selle astmefunktsiooni definitsioonipiirkonnaks intervalli - ∞; + ∞ , mis näeb ette, et astendaja a on taandamatu murd. Praegu EI defineeri paljude algebrat ja analüüsipõhimõtteid käsitlevate õppeväljaannete autorid astmefunktsioone, kus eksponendiks on argumendi negatiivsete väärtuste paaritu nimetajaga murd. Edaspidi järgime täpselt seda seisukohta: võtame hulga [ 0 ; + ∞) . Soovitus õpilastele: eriarvamuste vältimiseks uurige õpetaja seisukohta selles küsimuses.

Niisiis, vaatame võimsusfunktsiooni y = x a , kui eksponendiks on ratsionaal- või irratsionaalarv, eeldusel, et 0< a < 1 .

Illustreerime võimsusfunktsioone graafikutega y = x a, kui a = 11 12 (graafiline värv must); a = 5 7 (graafiku punane värv); a = 1 3 (graafiku sinine värv); a = 2 5 (graafiku roheline värv).

Eksponendi a muud väärtused (kui 0< a < 1) дадут аналогичный вид графика.

Definitsioon 10

Võimsusfunktsiooni omadused 0 juures< a < 1:

vahemik: y ∈ [ 0 ; + ∞) ;
funktsioon kasvab x ∈ [ 0 ; + ∞) ;
funktsioon on kumer x ∈ (0 ; + ∞) korral;
pöördepunktid puuduvad;
asümptoote pole;

Analüüsime võimsusfunktsiooni y = x a, kui eksponendiks on mittetäisarvuline ratsionaal- või irratsionaalarv, eeldusel, et a > 1.

Illustreerime graafikutega võimsusfunktsiooni y = x a antud tingimustel, kasutades näitena järgmisi funktsioone: y = x 5 4, y = x 4 3, y = x 7 3, y = x 3 π (vastavalt mustad, punased, sinised, rohelised graafikud).

Eksponendi a muud väärtused, kui a > 1, annavad sarnase graafiku.

Definitsioon 11

Võimsusfunktsiooni omadused > 1 korral:

määratluspiirkond: x ∈ [ 0 ; + ∞) ;
vahemik: y ∈ [ 0 ; + ∞) ;
see funktsioon on üldvormi funktsioon (see ei ole paaritu ega paaris);
funktsioon kasvab x ∈ [ 0 ; + ∞) ;
funktsioonil on nõgusus x ∈ (0 ; + ∞) jaoks (kui 1< a < 2) и выпуклость при x ∈ [ 0 ; + ∞) (когда a > 2);
pöördepunktid puuduvad;
asümptoote pole;
funktsiooni läbimispunktid: (0 ; 0) , (1 ; 1) .

Pange tähele, et kui a on paaritu nimetajaga negatiivne murd, on mõne autori teostes vaade, et määratluspiirkond asub! sel juhul– intervall - ∞; 0 ∪ (0 ; + ∞) hoiatusega, et astendaja a on taandamatu murd. Praegu autorid õppematerjalid algebras ja analüüsipõhimõtetes EI MÄÄRATA võimsusfunktsioone, mille astendaja on argumendi negatiivsete väärtuste jaoks paaritu nimetajaga murdosa. Lisaks järgime täpselt seda seisukohta: me võtame hulga (0 ; + ∞) murdosa negatiivsete eksponentide astmefunktsioonide definitsioonipiirkonnaks. Soovitus õpilastele: lahkarvamuste vältimiseks täpsustage siinkohal oma õpetaja nägemust.

Jätkame teemat ja analüüsime võimsusfunktsiooni y = x a tingimusel: - 1< a < 0 .

Toome välja järgmiste funktsioonide graafikud: y = x - 5 6, y = x - 2 3, y = x - 1 2 2, y = x - 1 7 (must, punane, sinine, roheline värv vastavalt jooned).

Definitsioon 12

Võimsusfunktsiooni omadused – 1< a < 0:

lim x → 0 + 0 x a = + ∞, kui - 1< a < 0 , т.е. х = 0 – вертикальная асимптота;

vahemik: y ∈ 0 ; + ∞ ;
see funktsioon on üldvormi funktsioon (see ei ole paaritu ega paaris);
pöördepunktid puuduvad;

Alloleval joonisel on kujutatud astmefunktsioonide y = x - 5 4, y = x - 5 3, y = x - 6, y = x - 24 7 graafikud (vastavalt must, punane, sinine, kõverate roheline värv).

Definitsioon 13

Võimsusfunktsiooni omadused a jaoks< - 1:

määratluspiirkond: x ∈ 0 ; + ∞ ;

lim x → 0 + 0 x a = + ∞ kui a< - 1 , т.е. х = 0 – вертикальная асимптота;

vahemik: y ∈ (0 ; + ∞) ;
see funktsioon on üldvormi funktsioon (see ei ole paaritu ega paaris);
funktsioon on kahanev x ∈ 0 korral; + ∞ ;
funktsioonil on nõgusus x ∈ 0 korral; + ∞ ;
pöördepunktid puuduvad;
horisontaalne asümptoot – sirge y = 0;
funktsiooni läbimise punkt: (1; 1) .

Kui a = 0 ja x ≠ 0, saame funktsiooni y = x 0 = 1, mis defineerib sirge, millest punkt (0; 1) välja jäetakse (lepiti kokku, et avaldisele 0 0 ei anta mingit tähendust ).

Eksponentfunktsioonil on vorm y = a x, kus a > 0 ja a ≠ 1 ning selle funktsiooni graafik näeb aluse a väärtuse põhjal välja erinev. Vaatleme erijuhtumeid.

Kõigepealt vaatame olukorda, kui eksponentsiaalfunktsiooni baasil on väärtus nullist üheni (0< a < 1) . Hea näide on funktsioonide graafikud a = 1 2 (kõvera sinine värv) ja a = 5 6 (kõvera punane värv) jaoks.

Eksponentfunktsiooni graafikud näevad tingimusel 0 sarnast välja ka teiste baasväärtuste puhul< a < 1 .

Definitsioon 14

Eksponentfunktsiooni omadused, kui alus on väiksem kui üks:

vahemik: y ∈ (0 ; + ∞) ;
see funktsioon on üldvormi funktsioon (see ei ole paaritu ega paaris);
eksponentsiaalfunktsioon, mille baas on väiksem kui üks, väheneb kogu määratluspiirkonna ulatuses;
pöördepunktid puuduvad;
horisontaalne asümptoot – sirge y = 0 muutujaga x kaldub + ∞;

Vaatleme nüüd juhtumit, kui eksponentsiaalfunktsiooni alus on suurem kui üks (a > 1).

Illustreerime seda erijuhtum eksponentsiaalfunktsioonide graafik y = 3 2 x (kõvera sinine värv) ja y = e x (graafiku punane värv).

Teised aluse väärtused, suuremad ühikud, annavad eksponentsiaalfunktsiooni graafikule sarnase välimuse.

Definitsioon 15

Eksponentfunktsiooni omadused, kui alus on suurem kui üks:

määratluspiirkond – reaalarvude kogum;
vahemik: y ∈ (0 ; + ∞) ;
see funktsioon on üldvormi funktsioon (see ei ole paaritu ega paaris);
eksponentsiaalfunktsioon, mille baas on suurem kui üks, kasvab kui x ∈ - ∞; + ∞ ;
funktsioonil on x ∈ - ∞ nõgusus; + ∞ ;
pöördepunktid puuduvad;
horisontaalne asümptoot – sirge y = 0 muutujaga x kaldub - ∞;
funktsiooni läbimise punkt: (0; 1) .

Logaritmiline funktsioon on kujul y = log a (x), kus a > 0, a ≠ 1.

Selline funktsioon on defineeritud ainult argumendi positiivsete väärtuste jaoks: x ∈ 0 korral; + ∞ .

Logaritmilise funktsiooni graafikul on erinevat tüüpi, mis põhineb aluse a väärtusel.

Vaatleme esmalt olukorda, kui 0< a < 1 . Продемонстрируем этот частный случай графиком логарифмической функции при a = 1 2 (синий цвет кривой) и а = 5 6 (красный цвет кривой).

Muud aluse väärtused, mitte suuremad ühikud, annavad sarnast tüüpi graafiku.

Definitsioon 16

Logaritmilise funktsiooni omadused, kui alus on väiksem kui üks:

määratluspiirkond: x ∈ 0 ; + ∞ . Kuna x kaldub paremalt nulli, kipuvad funktsiooni väärtused +∞;
väärtuste vahemik: y ∈ - ∞ ; + ∞ ;
see funktsioon on üldvormi funktsioon (see ei ole paaritu ega paaris);
logaritmiline
funktsioonil on nõgusus x ∈ 0 korral; + ∞ ;
pöördepunktid puuduvad;
asümptoote pole;

Vaatame nüüd erijuhtu, kui logaritmilise funktsiooni alus on suurem kui üks: a > 1 . Alloleval joonisel on kujutatud logaritmiliste funktsioonide y = log 3 2 x ja y = ln x graafikud (vastavalt graafikute sinine ja punane värv).

Teised aluse väärtused, mis on suuremad kui üks, annavad sarnast tüüpi graafiku.

Definitsioon 17

Logaritmilise funktsiooni omadused, kui alus on suurem kui üks:

määratluspiirkond: x ∈ 0 ; + ∞ . Kuna x kaldub paremalt nulli, kipuvad funktsiooni väärtused - ∞ ;
vahemik: y ∈ - ∞ ; + ∞ (kogu reaalarvude hulk);
see funktsioon on üldvormi funktsioon (see ei ole paaritu ega paaris);
logaritmiline funktsioon kasvab x ∈ 0 korral; + ∞ ;
funktsioon on kumer x ∈ 0 korral; + ∞ ;
pöördepunktid puuduvad;
asümptoote pole;
funktsiooni läbimise punkt: (1; 0) .

Trigonomeetrilised funktsioonid on siinus, koosinus, puutuja ja kotangens. Vaatame nende igaühe omadusi ja vastavat graafikat.

Üldiselt iseloomustab kõiki trigonomeetrilisi funktsioone perioodilisuse omadus, s.t. kui funktsiooni väärtusi korratakse juures erinevaid tähendusi argumendid, mis erinevad üksteisest perioodi võrra f (x + T) = f (x) (T – periood). Seega lisatakse trigonomeetriliste funktsioonide omaduste loendisse üksus “väikseim positiivne periood”. Lisaks näitame argumendi väärtused, mille juures vastav funktsioon muutub nulliks.

Siinusfunktsioon: y = sin(x)

Selle funktsiooni graafikut nimetatakse siinuslaineks.

Definitsioon 18

Siinuse funktsiooni omadused:

määratluspiirkond: kogu reaalarvude hulk x ∈ - ∞ ; + ∞ ;
funktsioon kaob, kui x = π · k, kus k ∈ Z (Z on täisarvude hulk);
funktsioon kasvab x ∈ - π 2 + 2 π · k korral; π 2 + 2 π · k, k ∈ Z ja kahanevalt x ∈ π 2 + 2 π · k korral; 3 π 2 + 2 π · k, k ∈ Z;
siinusfunktsioonil on lokaalsed maksimumid punktides π 2 + 2 π · k; 1 ja kohalikud miinimumid punktides - π 2 + 2 π · k; - 1, k ∈ Z;
siinusfunktsioon on nõgus, kui x ∈ - π + 2 π · k ; 2 π · k, k ∈ Z ja kumer, kui x ∈ 2 π · k; π + 2 π k, k ∈ Z;
asümptoote pole.

Koosinusfunktsioon: y = cos(x)

Selle funktsiooni graafikut nimetatakse koosinuslaineks.

Definitsioon 19

Koosinusfunktsiooni omadused:

määratluspiirkond: x ∈ - ∞ ; + ∞ ;
väikseim positiivne periood: T = 2 π;
väärtuste vahemik: y ∈ - 1 ; 1 ;
see funktsioon on paaris, kuna y (- x) = y (x);
funktsioon kasvab x ∈ - π + 2 π · k korral; 2 π · k, k ∈ Z ja kahanev x ∈ 2 π · k korral; π + 2 π k, k ∈ Z;
koosinusfunktsioonil on lokaalsed maksimumid punktides 2 π · k ; 1, k ∈ Z ja lokaalsed miinimumid punktides π + 2 π · k; - 1, k ∈ z;
koosinusfunktsioon on nõgus, kui x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π · k , k ∈ Z ja kumer kui x ∈ - π 2 + 2 π · k ; π 2 + 2 π · k, k ∈ Z;
käändepunktide koordinaadid on π 2 + π · k; 0, k ∈ Z
asümptoote pole.

Tangensi funktsioon: y = t g (x)

Selle funktsiooni graafikut nimetatakse puutuja.

Definitsioon 20

Tangensi funktsiooni omadused:

määratluspiirkond: x ∈ - π 2 + π · k ; π 2 + π · k, kus k ∈ Z (Z on täisarvude hulk);
Tangensi funktsiooni käitumine piirkonna piiril lim määratlused x → π 2 + π · k + 0 t g (x) = - ∞ , lim x → π 2 + π · k - 0 t g (x) = + ∞ . Seega on sirgjooned x = π 2 + π · k k ∈ Z vertikaalsed asümptoodid;
funktsioon kaob, kui x = π · k k ∈ Z korral (Z on täisarvude hulk);
väärtuste vahemik: y ∈ - ∞ ; + ∞ ;
see funktsioon on paaritu, kuna y (- x) = - y (x) ;
funktsioon kasvab kui - π 2 + π · k ; π 2 + π · k, k ∈ Z;
puutujafunktsioon on nõgus x ∈ [π · k korral; π 2 + π · k) , k ∈ Z ja kumer x ∈ jaoks (- π 2 + π · k ; π · k ] , k ∈ Z ;
käändepunktidel on koordinaadid π · k ; 0, k ∈ Z;

Kotangentne funktsioon: y = c t g (x)

Selle funktsiooni graafikut nimetatakse kotangentoidiks. .

Definitsioon 21

Kootangensfunktsiooni omadused:

määratluspiirkond: x ∈ (π · k ; π + π · k) , kus k ∈ Z (Z on täisarvude hulk);

Kootangensfunktsiooni käitumine definitsioonipiirkonna lim x → π · k + 0 t g (x) = + ∞ piiril, lim x → π · k - 0 t g (x) = - ∞ . Seega sirged x = π · k k ∈ Z on vertikaalsed asümptoodid;

väikseim positiivne periood: T = π;
funktsioon kaob, kui x = π 2 + π · k k ∈ Z korral (Z on täisarvude hulk);
väärtuste vahemik: y ∈ - ∞ ; + ∞ ;
see funktsioon on paaritu, kuna y (- x) = - y (x) ;
funktsioon on kahanev x ∈ π · k korral; π + π k, k ∈ Z;
kotangensfunktsioon on x ∈ korral nõgus (π · k; π 2 + π · k ], k ∈ Z ja kumer x ∈ [ - π 2 + π · k ; π · k), k ∈ Z korral;
käändepunktide koordinaadid on π 2 + π · k; 0, k ∈ Z;
Puuduvad kaldus või horisontaalsed asümptootid.

Trigonomeetrilised pöördfunktsioonid on arcsinus, arkosiinus, arktangent ja arkotangens. Sageli nimetatakse eesliite "kaar" olemasolu tõttu nimes trigonomeetrilisi pöördfunktsioone kaarefunktsioonideks. .

Kaarsiinuse funktsioon: y = a r c sin (x)

Definitsioon 22

Arsiinuse funktsiooni omadused:

see funktsioon on paaritu, kuna y (- x) = - y (x) ;
arcsinusfunktsioonil on x ∈ 0 korral nõgusus; 1 ja kumerus x ∈ - 1 korral; 0 ;
käändepunktidel on koordinaadid (0; 0), mis on ühtlasi funktsiooni null;
asümptoote pole.

Kaarkoosinuse funktsioon: y = a r c cos (x)

Definitsioon 23

Kaarkoosinusfunktsiooni omadused:

määratluspiirkond: x ∈ - 1 ; 1 ;
vahemik: y ∈ 0 ; π;
see funktsioon on üldkujuline (ei paaris ega paaritu);
funktsioon väheneb kogu definitsioonipiirkonna ulatuses;
kaarekoosinusfunktsioonil on x ∈ - 1 nõgusus; 0 ja kumerus x ∈ 0 korral; 1 ;
käändepunktide koordinaadid on 0; π2;
asümptoote pole.

Kaartangensi funktsioon: y = a r c t g (x)

Definitsioon 24

Arktangensi funktsiooni omadused:

määratluspiirkond: x ∈ - ∞ ; + ∞ ;
väärtuste vahemik: y ∈ - π 2 ; π2;
see funktsioon on paaritu, kuna y (- x) = - y (x) ;
funktsioon kasvab kogu definitsioonipiirkonna ulatuses;
arktangensfunktsioonil on x ∈ jaoks nõgusus (- ∞ ; 0 ] ja kumerus x ∈ [ 0 ; + ∞ );
käändepunktil on koordinaadid (0; 0), mis on ühtlasi funktsiooni null;
horisontaalsed asümptoodid on sirged y = - π 2 kui x → - ∞ ja y = π 2 kui x → + ∞ (joonisel on asümptoodid rohelised jooned).

Kaartangensi funktsioon: y = a r c c t g (x)

Definitsioon 25

Arkotangensi funktsiooni omadused:

määratluspiirkond: x ∈ - ∞ ; + ∞ ;
vahemik: y ∈ (0; π) ;
see funktsioon on üldkujul;
funktsioon väheneb kogu definitsioonipiirkonna ulatuses;
kaare kotangensi funktsioonil on nõgusus x ∈ [ 0 ; + ∞) ja kumerus x ∈ jaoks (- ∞ ; 0 ] ;
käändepunkti koordinaadid on 0; π2;
horisontaalsed asümptoodid on sirged y = π punktis x → - ∞ (joonisel roheline joon) ja y = 0 punktis x → + ∞.

Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter

Ehitamise funktsioon

Pakume teie tähelepanu funktsioonide graafikute koostamise teenust Internetis, mille kõik õigused kuuluvad ettevõttele Desmos. Funktsioonide sisestamiseks kasutage vasakpoolset veergu. Saate sisestada käsitsi või kasutades virtuaalset klaviatuuri akna allosas. Akna suurendamiseks graafikuga saate peita nii vasaku veeru kui ka virtuaalse klaviatuuri.

Veebikaardistamise eelised

Sisestatud funktsioonide visuaalne kuvamine
Väga keeruliste graafikute koostamine
Kaudselt määratud graafikute koostamine (näiteks ellips x^2/9+y^2/16=1)
Võimalus salvestada diagramme ja saada neile link, mis muutub Internetis kõigile kättesaadavaks
Skaala, joone värvi juhtimine
Võimalus joonistada graafikuid punktide kaupa, kasutades konstante
Mitme funktsioonigraafiku joonistamine samaaegselt
Joonistamine polaarkoordinaatides (kasutage r ja θ(\theta))

Meiega on veebis lihtne koostada erineva keerukusega graafikuid. Ehitus tehakse koheselt. Teenus on nõutud funktsioonide ristumispunktide leidmiseks, graafikute kujutamiseks nende edasiseks Wordi dokumenti teisaldamiseks ülesannete lahendamisel illustratsioonidena ning funktsioonigraafikute käitumistunnuste analüüsimiseks. Optimaalne brauser saidi sellel lehel diagrammidega töötamiseks on Google Chrome. Teiste brauserite kasutamisel pole korrektne toimimine garanteeritud.

1) Funktsiooni domeen ja funktsioonide vahemik.

Funktsiooni domeen on kõigi kehtivate kehtivate argumentide väärtuste kogum x(muutuja x), mille jaoks funktsioon y = f(x) kindlaks määratud. Funktsiooni vahemik on kõigi reaalväärtuste hulk y, mille funktsioon aktsepteerib.

Elementaarmatemaatikas uuritakse funktsioone ainult reaalarvude hulgal.

2) Funktsiooni nullid.

Funktsioon null on argumendi väärtus, mille juures funktsiooni väärtus võrdub nulliga.

3) Funktsiooni konstantse märgi intervallid.

Funktsiooni konstantse märgi intervallid on argumentide väärtuste komplektid, mille funktsiooni väärtused on ainult positiivsed või ainult negatiivsed.

4) Funktsiooni monotoonsus.

Kasvav funktsioon (teatud intervallis) on funktsioon, mille jaoks kõrgem väärtus selle intervalli argument vastab funktsiooni suuremale väärtusele.

Vähenev funktsioon (teatud intervallis) on funktsioon, milles selle intervalli argumendi suurem väärtus vastab funktsiooni väiksemale väärtusele.

5) Paaris (paaritu) funktsioon.

Paarisfunktsioon on funktsioon, mille määratluspiirkond on sümmeetriline lähtekoha suhtes ja mis tahes jaoks X määratlusvaldkonnast võrdsus f(-x) = f(x). Paarisfunktsiooni graafik on ordinaadi suhtes sümmeetriline.

Paaritu funktsioon on funktsioon, mille määratluspiirkond on sümmeetriline lähtekoha suhtes ja mis tahes jaoks X definitsiooni valdkonnast on võrdsus tõene f(-x) = - f(x). Paaritu funktsiooni graafik on algpunkti suhtes sümmeetriline.

6) Piiratud ja piiramatud funktsioonid.

Funktsiooni nimetatakse piiritletuks, kui on olemas positiivne arv M, mille puhul |f(x)| ≤ M kõigi x väärtuste korral. Kui sellist numbrit pole, on funktsioon piiramatu.

7) Funktsiooni perioodilisus.

Funktsioon f(x) on perioodiline, kui on olemas nullist erinev arv T, nii et mis tahes funktsiooni definitsioonipiirkonna x korral kehtib järgmine: f(x+T) = f(x). Seda väikseimat arvu nimetatakse funktsiooni perioodiks. Kõik trigonomeetrilised funktsioonid on perioodilised. (Trigonomeetrilised valemid).

19. Põhilised elementaarfunktsioonid, nende omadused ja graafikud. Funktsioonide rakendamine majanduses.

Põhilised elementaarfunktsioonid. Nende omadused ja graafikud

1. Lineaarne funktsioon.

Lineaarne funktsioon nimetatakse funktsiooniks kujul , kus x on muutuja, a ja b on reaalarvud.

Number A mida nimetatakse sirge kaldeks, on see võrdne selle sirge kaldenurga puutujaga abstsisstelje positiivse suuna suhtes. Lineaarfunktsiooni graafik on sirgjoon. See on määratletud kahe punktiga.

Lineaarse funktsiooni omadused

1. Definitsioonipiirkond – kõigi reaalarvude hulk: D(y)=R

2. Väärtuste hulk on kõigi reaalarvude hulk: E(y)=R

3. Funktsioon võtab nullväärtuse, kui või.

4. Funktsioon suureneb (väheneb) kogu määratluspiirkonna ulatuses.

5. Lineaarfunktsioon on pidev kogu definitsioonipiirkonna ulatuses, diferentseeruv ja .

2. Ruutfunktsioon.

Vormi funktsiooni, kus x on muutuja, koefitsiendid a, b, c on reaalarvud, nimetatakse ruutkeskne

Koefitsiendid a, b, c määrata graafiku asukoht koordinaattasandil

Koefitsient a määrab okste suuna. Ruutfunktsiooni graafik on parabool. Parabooli tipu koordinaadid leitakse valemite abil:

Funktsiooni omadused:

2. Ühe intervalli väärtuste komplekt: või.

3. Funktsioon võtab nullväärtusi, kui , kus diskriminant arvutatakse valemiga:.

4. Funktsioon on pidev kogu definitsioonipiirkonna ulatuses ja funktsiooni tuletis on võrdne .

Toitefunktsioon. See on funktsioon: y = axn, Kus a, n- püsiv. Kell n= 1 saame otsene proportsionaalsus: y = kirves; juures n = 2 - ruudu parabool ; juures n = - 1 - pöördvõrdelisus või hüperbool. Seega on need funktsioonid võimsusfunktsiooni erijuhud. Teame, et iga nullist erineva arvu nullaste on 1, seega kl n= 0, muutub võimsusfunktsioon konstantseks väärtuseks:y = a, st. tema ajakava on sirgjoon, teljega paralleelne X, välja arvatud päritolu (täpsusta palun, Miks? ). Kõik need juhtumid (koos a= 1 ) näidatud joonisel 13 (n 0) ja joonis 14 ( n < 0). Отрицательные значения xsiin ei arvestata, seega nagu siis mõned funktsioonid:

Kui n– täisarv, astmefunktsioonid on mõistlikud isegi siis, kuix< 0, но их графики имеют различный вид в зависимости от того, является ли npaaris või paaritu arv. Joonisel 15 on näidatud kaks sellist võimsusfunktsiooni: Sest n= 2 ja n = 3.

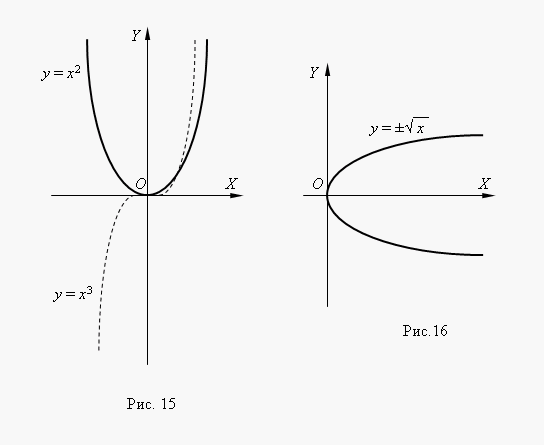
Kell n= 2 funktsioon on paaris jaselle graafik on sümmeetriline telje suhtes Y. Kell n= 3 funktsioon on paaritu ja selle graafik on algpunkti suhtes sümmeetriline koordinaadid Funktsioony = x 3 helistas kuupne parabool.

Joonis 16 näitab funktsiooni. See funktsioon on pöördvõrdeline ruutparabooliga y = x 2 , selle graafik saadakse ruutparabooli graafiku pööramisel ümber 1. koordinaatnurga poolitaja. See on viis mis tahes graafiku saamiseks pöördfunktsioon selle algse funktsiooni graafikult. Graafikult näeme, et tegemist on kahe väärtusega funktsiooniga (seda näitab ka ruutjuure ees olev ± märk). Selliseid funktsioone elementaarmatemaatikas ei uurita, seetõttu käsitleme funktsioonina tavaliselt üht selle haru: ülemist või alumist.

Põhilised elementaarfunktsioonid on: konstantne funktsioon (konstant), juur n-th aste, astmefunktsioon, eksponentsiaal-, logaritmifunktsioon, trigonomeetrilised ja pöördtrigonomeetrilised funktsioonid.

Püsiv funktsioon.

Konstantne funktsioon on antud kõigi reaalarvude hulgale valemiga , kus C- mõni reaalarv. Konstantne funktsioon määrab sõltumatu muutuja iga tegeliku väärtuse x sõltuva muutuja sama väärtus y- tähendus KOOS. Konstantset funktsiooni nimetatakse ka konstandiks.

Konstantse funktsiooni graafik on x-teljega paralleelne ja koordinaatidega punkti läbiv sirge (0,C). Näiteks näitame konstantsete funktsioonide graafikuid y=5,y=-2 ja , mis alloleval joonisel vastavad vastavalt mustale, punasele ja sinisele joonele.

Konstantse funktsiooni omadused.

Domeen: kogu reaalarvude komplekt.

Konstantne funktsioon on ühtlane.

Väärtuste vahemik: ainsuse arvust koosnev hulk KOOS.

Konstantne funktsioon ei suurene ega kahane (sellepärast on see konstantne).

Konstandi kumerusest ja nõgususest pole mõtet rääkida.

Asümptoote pole.

Funktsioon läbib punkti (0,C) koordinaattasand.

N-nda astme juur.

Vaatleme põhielementaarfunktsiooni, mis on antud valemiga, kus n– ühest suurem naturaalarv.

n-s juur, n on paarisarv.

Alustame juurfunktsiooniga n-th aste juureksponenti paarisväärtuste jaoks n.

Siin on näiteks pilt funktsioonigraafikute piltidega ja , need vastavad mustale, punasele ja sinisele joonele.

Paarisastme juurfunktsioonide graafikud on eksponendi teiste väärtuste puhul sarnased.

Juurefunktsiooni omadusedn -th võimu ühtlanen .

N-s juur n on paaritu arv.

Juurefunktsioon n-th aste paaritu juureksponentiga n on defineeritud kogu reaalarvude hulga kohta. Näiteks siin on funktsioonide graafikud ja , vastavad mustale, punasele ja sinisele kõverale.

Teiste juureksponenti paaritute väärtuste puhul on funktsioonigraafikud sarnased.

Juurefunktsiooni omadusedn - paaritu asten .